The last couple of years interesting but not so popular paradigm appears more often. I’m talking about Data Oriented Design (DOD). If you’re searching for a job that involves high-performance calculations be ready to hear corresponding questions. And I was surprised knowing that some my colleagues have never heard about the approach and after the short discussion stayed skeptical. In this article I’ll try to compare traditional OOP approach with DOD on a real world example.
What is DOD?
This post is an attempt to compare different programming approach without trying to explain them. I assume you know what we’ll talk about. There’re a lot of articles on the web about the subject. This one is good. This video from CppCon also is a must see. But in layman’s terms, DOD is a way to work with data in cache friendly manner. Better see an example:
#include <chrono>
#include <iostream>
#include <vector>
using namespace std;
using namespace std::chrono;
struct S
{
uint64_t u;
double d;
int i;
float f;
};
struct Data
{
vector<uint64_t> vu;
vector<double> vd;
vector<int> vi;
vector<float> vf;
};
int test1(S const & s1, S const & s2)
{
return s1.i + s2.i;
}
int test2(Data const & data, size_t const ind1, size_t const ind2)
{
return data.vi[ind1] + data.vi[ind2];
}
int main()
{
size_t const N{ 30000 };
size_t const R{ 10 };
vector<S> v(N);
Data data;
data.vu.resize(N);
data.vd.resize(N);
data.vi.resize(N);
data.vf.resize(N);
int result{ 0 };
cout << "test #1" << endl;
for (uint32_t i{ 0 }; i < R; ++i)
{
auto const start{ high_resolution_clock::now() };
for (size_t a{ 0 }; a < v.size() - 1; ++a)
{
for (size_t b{ a + 1 }; b < v.size(); ++b)
{
result += test1(v[a], v[b]);
}
}
cout << duration<float>{ high_resolution_clock::now() - start }.count() << endl;
}
cout << "test #2" << endl;
for (uint32_t i{ 0 }; i < R; ++i)
{
auto const start{ high_resolution_clock::now() };
for (size_t a{ 0 }; a < v.size() - 1; ++a)
{
for (size_t b{ a + 1 }; b < v.size(); ++b)
{
result += test2(data, a, b);
}
}
cout << duration<float>{ high_resolution_clock::now() - start }.count() << endl;
}
return result;
}The second test runs faster by 30% (in VS2017 and gcc7.0.1). But why?
The size of the S struct is 24 bytes. My CPU (Intel Core i7) have 32KB L1 cache for each core with 64B cache line. That means that when we’re requesting data from the main memory one cache line can hold only two full S structs at most. In the first test we’re reading only one int field, i.e. in the best case scenario one cache line can hold only two S::i (ok, sometimes three). In the second test we’re reading similar int but from the vector of integers. std::vector guarantees sequentiality of the data it holds. That means that one cache line can hold up to 16 (64KB / sizeof(int) = 16) values we need. Obviously, we’re communicating with the RAM less often. And it’s known that memory operations are the bottleneck in modern CPUs.
What about real life?
The example above clearly shows the benefits of SoA (Struct of Arrays) vs AoS (Array of Structures). But this example was from the Hello World category, i.e. it’s very far from real world applications. In reality, the code has lots of dependencies and specific data which probably will not give such performance increase. One more thing - if in our example we’ll read all fields of the struct there will be no difference in speed.
In order to understand possibility to apply DOD I decided to write more or less complex program with both (OOP and DOD) approaches. Let it be a 2d rigid body simulation - we’ll create N convex polygons with different parameters - mass, speed etc. - and we’ll see how many such objects we can simulate staying at 30 fps.
Array of Structures
Initial program
Source code for this version can be found in this commit and we briefly run through the code.
For simplicity reasons the program is written in Visual Studio for Windows and uses DirectX11 for rendering.
I’m using the latest VS2017 and some features of c++17, namely std::optional. Intersection detector takes two objects and returns by value a struct with intersection information - normal, penetration depth. Previously I used a boolean flag inside that structure that showed was there an intersection at all. With the new
std::optionalI got rid of that flag and the code became more clear.
The purpose of this article is to show some numbers on CPU so we’ll not discuss graphics.
The Shape class which represents physical body looks like this (simplified):
class Shape
{
public:
math::Vec2 position{ 0.0f, 0.0f };
math::Vec2 velocity{ 0.0f, 0.0f };
math::Vec2 overlapResolveAccumulator{ 0.0f, 0.0f };
float massInverse;
math::Color color;
std::vector<math::Vec2> vertices;
math::Bounds bounds;
};- I believe
positionandvelocityfields don’t need a discussion vertices— a random number of polygon verticesbounds— shape’s bounding box. Used for broad collision detectionmassInverse— one over mass (1 / m). We’ll use only this value so no need to keep mass itselfcolor— used for rendering but stored in shapeoverlapResolveAccumulator- see below.
From the structure, it’s already seen that
colornot used for calculations at all. But steel takes place in the cache line.
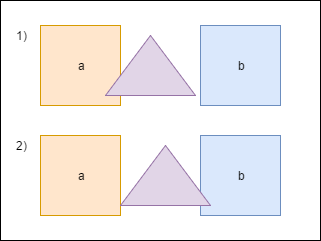

When the triangle intersects shape a we need to move it apart to avoid figures overlapping. Also, we have to recalculate bounds. But now the triangle intersects shape b and we need to repeat the procedure again - move the shape and recalculate bounds. Notice that after the second move the triangle again will be over shape a. To avoid this repetition we’ll store the value necessary to separate objects in special accumulator - overlapResolveAccumulator - and later will move the shape by this value but only once. Not physically correct at all, but looks ok. Notice also that this field also adds to the total size of the class which is not good for the memory.
The heart of our program is a ShapesApp::update() function. Here it’s simplified form:
void ShapesApp::update(float const dt)
{
float const dtStep{ dt / NUM_PHYSICS_STEPS };
for (uint32_t s{ 0 }; s < NUM_PHYSICS_STEPS; ++s)
{
updatePositions(dtStep);
for (size_t i{ 0 }; i < _shapes.size() - 1; ++i)
{
for (size_t j{ i + 1 }; j < _shapes.size(); ++j)
{
CollisionSolver::solveCollision(_shapes[i].get(), _shapes[j].get());
}
}
}
}Every frame we call a ShapesApp::updatePositions() function that updates every shape’s position and bounds. Next we check every shape with every other for collision in CollisionSolver::solveCollision() function. I used Separating Axis Theorem (SAT) for that. And we repeat these steps NUM_PHYSICS_STEPS times. This variable serves several purposes - first, the physics becomes more stable, and second, it limits the number of objects on the screen. c++ is fast, amazingly fast, and without this limitation we’ll have tens of thosands of objects which will lead to rendering performance issues. In my tests I used NUM_PHYSICS_STEPS = 20.
On my humble laptop this version of the program simulates 500 shapes before fps starts to drop below 30. Wat?? Only 500?? Even JavaScript can do better. I agree, not a lot, but don’t forget - we’re repeating calculations 20 times per frame.
I think I need to add some pictures to make the post not so boring, so here we go:
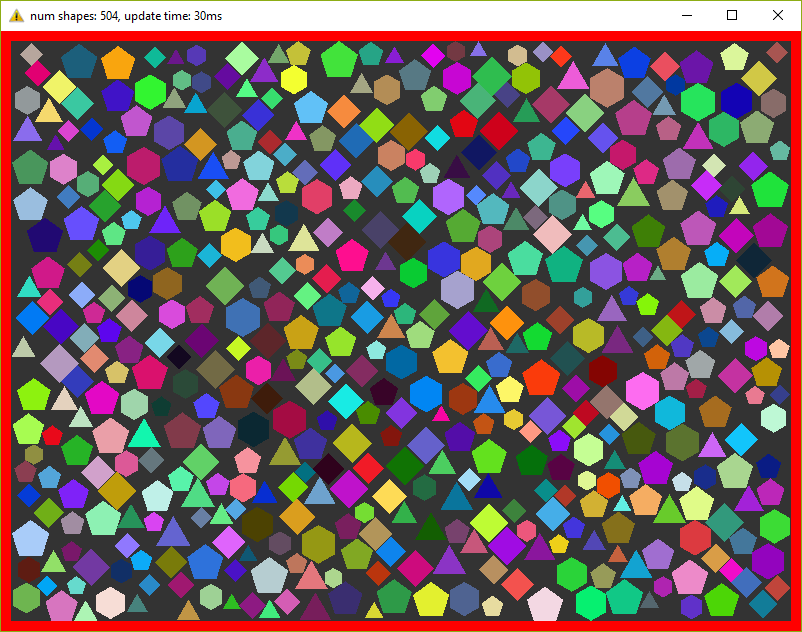

Optimization #1. Spatial Grid
I mentioned several times that I want to make tests on a program which is as close to real world as possible. Obviously, the code above is not usable - nobody checks each shape with each other - this is veeeery slow. For acceleration usually, some spetial spatial structure being used. We’ll use simple 2d grid - I called it Grid in the code - which consists of NxM cells - struct Cell. At the calculation start we’ll put each object in the corresponding cell. This way all we have to do is to iterate over cells and check intersection between several pairs of objects. I used the similar code a lot of times in real projects and it behaved very well. Besides, it’s very easy to implement, easy to debug and understand.
The commit for this version can be found here. We added a new entity - Grid and changed ShapesApp::update() function. Now it calls Grid’s methods for updating and intersections.
This version can simulate 8000 shapes now at 30 fps (don’t forget about 20 repetitions in each frame)! I had to decrease shape’s sizes in order to fit them in the window.
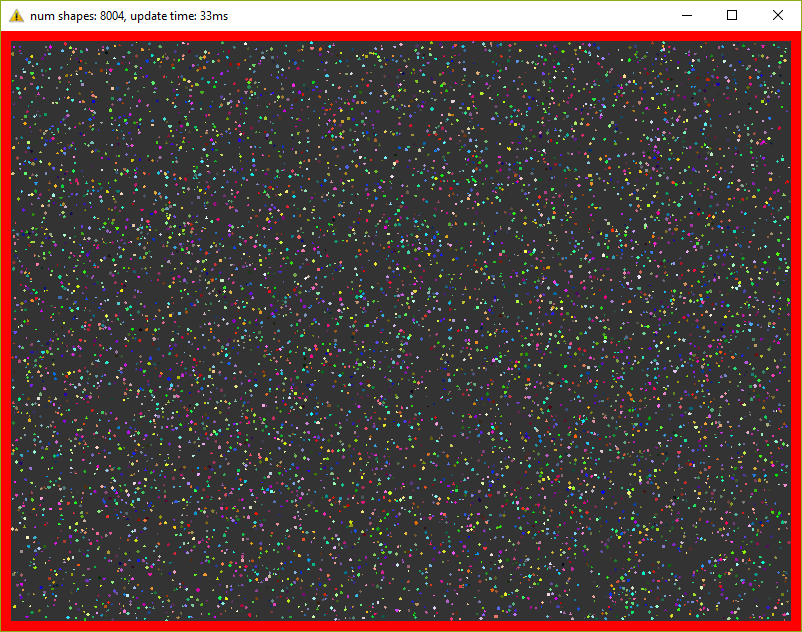

Optimization #2. Multithreading.
These days, when even cell phones have 4 cores inside, ignore multithreading is silly. In this, the last optimization we’ll add a thread pool and will divide main work by equal tasks. For example, ShapesApp::updatePositions() which iterated over all shapes before now iterates only over a part of the shapes on each core. Thread pool class was taken from here and the final version of the program you can find in this commit. In my tests, I used 4 threads (including main).
Dividing the work by tasks added some head pain. For example, if a shape crosses cell boundaries it will end in several cells at the same time.
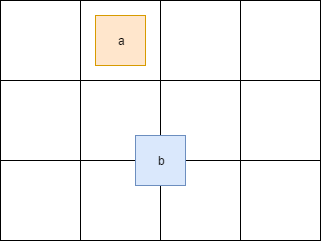

Here the shape a fully contained in one cell, but b is in 4 cells at the same time. Because of this, we have to synchronize cell access. Also, we have to synchronize access to some fields inside the Shape class. We can achieve this adding std::mutex to the Shape and Cell.
Now I can see 13000 shapes at 30 fps. For such amount of objects, I had to increase the window size. And I say it again - in every frame we’re repeating simulation 20 times.
To be honest this program has bad parallelization possibilities. That’s why increasing the number of threads will not give us a significant performance boost. But that’s another story.


Structure of Arrays
Initial program
The code we wrote above I call traditional OOP approach - I write such code many years and see similar code in general. But now we’ll modify it a little - we’ll remove class Shape and replace it with vectors and see can this tiny change affect the performance? To my happiness refactoring wasn’t hard, even trivial. Instead of the Shape class, we’ll use a struct with vectors of data.
struct ShapesData
{
std::vector<math::Vec2> positions;
std::vector<math::Vec2> velocities;
std::vector<math::Vec2> overlapAccumulators;
std::vector<float> massesInverses;
std::vector<math::Color> colors;
std::vector<std::vector<math::Vec2>> vertices;
std::vector<math::Bounds> bounds;
};We pass this struct like this - solveCollision(struct ShapesData & data, std::size_t const indA, std::size_t const indB). I.e. instead of shapes instances we pass indices and inside function necessary data is taking from the vectors.
This version of the program can simulate 500 objects at 30 fps. As you can see there’s no difference with the original version. This is because we have relatively small data set and the “heaviest” function uses almost all fields of the struct.
Further without pictures since they are the same.
Optimization #1. Spatial Grid
Everything as before except only we switch to SoA instead of AoS. The source code is here. The result is better - 9500 objects vs 8000 before, i.e. the performance difference is around 15%.
Optimization #2. Multithreading.
Again take the old code, switch structs and get 15000 objects at 30 fps. Again performance increase is around 15%. Here’s the final version of the program.
Conclusion
I satisfied with the results. As you can see the small change in the code can lead to the quite big performance boost. But not always. It’s even possible to lose some speed. For example, if we need only one instance of a class then with a traditional approach we read the data from memory once and have an access to all fields. On the other side if we read each field individually via vectors we have cache miss on each reading. Moreover, the general readability and complexity become worse.
As usual, it’s hard to give an unambiguous answer - should everybody switch to the new paradigm? When I worked on a 3d game engine 10% performance increase was a huge number. But when I worked on game launcher, mostly UI, then usage of this approach would only cause bewilderment of my colleagues. As general advice - profile, measure and decide yourself.